Watch the video below to briefly learn about Kepler’s Laws in an animated format.
First Law
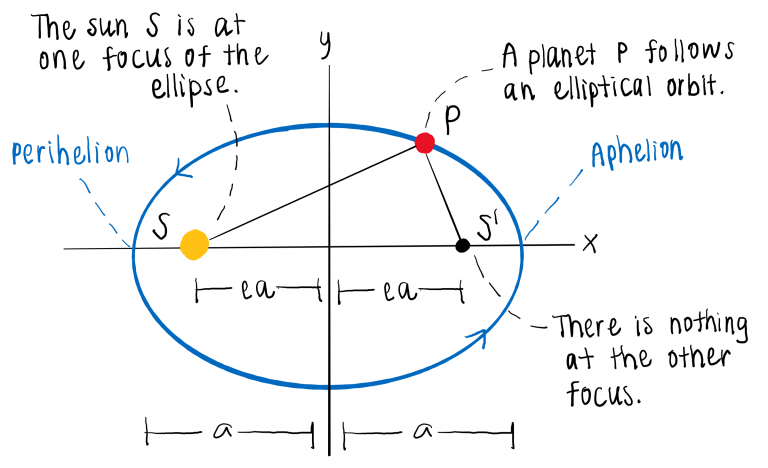
Planets move in elliptical orbits with the sun at one focus of the ellipse.
An ellipse is a regular oval shape. The longest dimension of an ellipse is known as the major axis, while the half-length is semi-major axis.
There are two foci (singular: focus), which are fixed points on the major axis, spaced equally from the center. This distance from the center to the focus of the ellipse is ea, where e measures eccentricity. Eccentricity defines how circular the orbit is; if e=0, the two foci overlap and the ellipse is a circle.
Second Law
A given planet covers the same area of space in the same amount of time, regardless of orbit location.
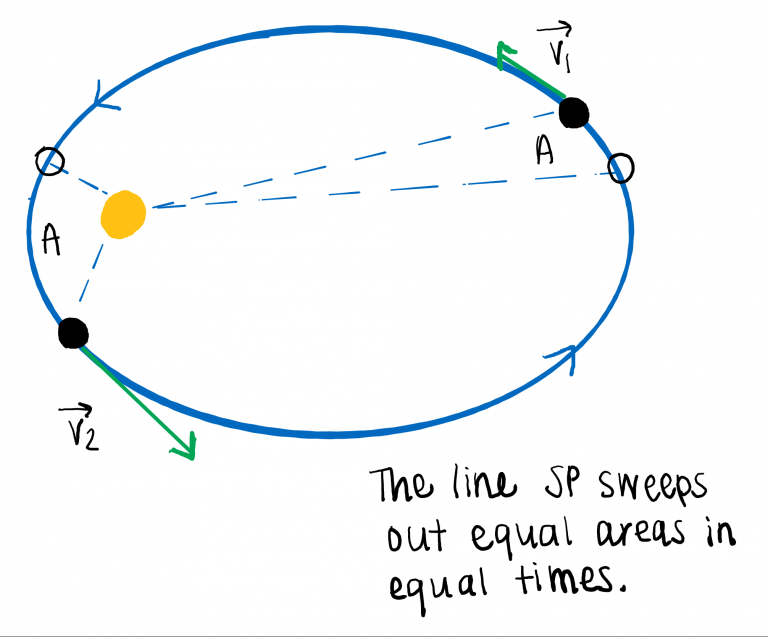
Sector velocity is the rate at which the area A is swept out. A planet moves fastest in orbit when it is closest to the sun and slowest when it is furthest from the sun. Despite changes in speed, sector velocity is the same at all points in the orbit. This means that the same amount of area is swept out by line SP in equal periods of time.
Third Law
The average distance of a planet from the sun cubed is proportional to the orbital period squared.
Kepler’s third law is represented by the equation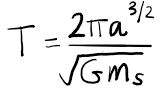
for an elliptical orbit around the sun, where T is the orbital period, ms is the mass of the sun, G is the gravitational constant, and a is the semi-major axis (see the figure in Kepler’s first law column).
As you can see, the orbital period does not depend on eccentricity e. This means that a planet with a longer elliptical orbit will have the same orbital period as a planet with a circular orbit.
How exactly does that work, though?
The planet in an elongated elliptical orbit moves at different speeds at different points. Speed is greatest at perihelion and slowest at aphelion. In a circular orbit, speed is constant. The differences in speed and orbital shape result in the same orbital period for both planets.
