Before we explore Newton’s 2nd law of motion, let’s define some of the terms involved!
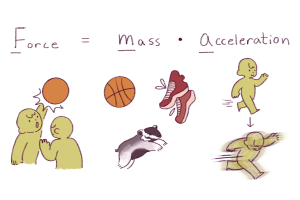
Force is an interaction that can change the motion of an object. Its standard unit of measurement is Newtons (N).
Mass is a quality that all objects have, and it is a measure of the matter in an object. It is not the same thing as an object’s weight, which varies based on the gravity the object experiences. Its standard unit of measurement is kilograms (kg).
Acceleration is the change in velocity of an object in motion (“speeding up,” or “slowing down”). Like velocity, acceleration occurs in a specific direction. Its standard unit of measurement is meters per second^2 (m/s^2).
The relationship between force, mass, and acceleration is described in Newton’s 2nd law of motion:

Newton’s 2nd law of motion: if an object encounters a net force, then the acceleration of that object is directly proportional to that force. In other words, force = mass • acceleration.
From force = mass • acceleration, changing any of those three variables will change an object’s motion. Any change in force is proportional to a change in mass and/or acceleration, and any change in mass is inversely proportional to a change in acceleration (and vice versa). For example, if an object of mass m is replaced by an object with double the mass, 2m, you would need twice the force to move the larger mass at the same acceleration as the smaller mass. Or, of you wanted to apply the same force to both masses, the 2m mass would have to move at half the acceleration as m.
Because both acceleration and force are vector quantities (meaning they have a specific direction) changing the direction of a force will also result in a change in the direction of acceleration.

Another quality of vectors is that they can be defined by their horizontal and vertical components. The horizontal movement of an object does not impact its vertical movement, and the vertical movement of an object does not impact its horizontal movement. The vector components can be depicted as two sides of a right triangle, with the hypotenuse being the vector itself.
Using Newton’s 2nd law, answer the question below. For the first two questions, ignore the effects of gravity and air resistance.
This is an accordion element with a series of buttons that open and close related content panels.
If the ball has a mass of 1.50 kg and is thrown forward horizontally with a force of 20.0 N, what is its horizontal acceleration?
13.3 m/s^2 forward
If F = ma, then in this example 20 N = 1.5 kg*a. Solving for a gives 13.3 m/s^2.
The same 1.50 kg ball is caught by a player directly the court, but this player throws it with twice the force as the first player. What is the change in the magnitude of the ball's acceleration, in terms of a?
The acceleration doubles (2a).
Force is proportional to mass and acceleration; if force is doubled, acceleration is also doubled.
Note that acceleration is inversely proportional to mass. Rearranging the equation gives a = F/m, meaning that an increase in mass leads to a proportional decrease in acceleration.
Let's consider gravity again! If two 1.50 kg balls are thrown horizontally, one with a force of 13.3 N and another with a force of 22.5 N, which one accelerates to the ground faster?
Their downwards acceleration is the same.
Because force and acceleration are vector quantities, their horizontal motion and vertical motion can be considered separately. The balls’ horizontal forces and acceleration do not impact how fast they fall vertically. If gravity is the only force acting in the vertical direction, what matters is the balls’ mass, the force of gravity (their weight), and the acceleration due to gravity (which is 9.81 m/s^2 on Earth).